本文共计1995个文字,预计阅读时间需要6分30秒,欢迎阅读借鉴、一起学习、进步,内容来自小编精心整理收集,如有不正确和疑问,欢迎指正。
请问lnx^2的定义域为什么和lnx的定义域不一样
对函数f(x)=lnx,定义域要求x∈(0,+∞),而ln(x²),要求x²>0,即x∈(-∞,0)U(0,+∞),所以两者定义域不同。lnx为分母定义域是多少?
lnx为分母定义域是多少?
lnx为分母定义域是{x|x>0,且x≠1}。
对于这种问题,就需要熟悉对数的定义,以及对数的相关运算法则。
对数函数的图像与性质。
分式有意义,分母要求不等于零等。
并且能够强到恰当的应用相关知识来解决问题。应当注意运算。
下面分享相关内容的知识扩展:
lnx是偶函数还是奇函数?
y=lnx是非奇非偶函数,因为定义域:(0,+无穷)不关于原点对成昆,所以是非奇非偶函数。自然对数是以常数e为底数的对数,记作lnN(N>0)。在物理学,生物学等自然科学中有重要的意义,一般表示方法为lnx。数学中也常见以logx表示自然对数。
lnx的取值范围?以及关于ln的所有公式?
lnx<=0.得出 X>=e分之一。lnx>=-1,得出 0<X<=-1 .
都是根据什么得出的?
我现在就知道lnE=1 ln1=0
还有其他关于LN的公式以及常用的运算吗?
一般地,如果a(a大于0,且a不等于1)的b次幂等于N,那么数b叫做以a为底N的对数,记作log(a)(N)=b,其中a叫做对数的底数,N叫做真数。
底数则要大于0且不为1 真数大于0
对数的运算性质:
当a>0且a≠1时,M>0,N>0,那么:
(1)log(a)(MN)=log(a)(M)+log(a)(N);
(2)log(a)(M/N)=log(a)(M)-log(a)(N);
(3)log(a)(M^n)=nlog(a)(M) (n∈R)
(4)换底公式:log(A)M=log(b)M/log(b)A (b>0且b≠1) (5) a^(log(b)n)=n^(log(b)a) 证明尚没找到,出处在《算法导论》(第一版)公式(2.9)
对数与指数之间的关系
当a>0且a≠1时,a^x=N x=㏒(a)N (对数恒等式)
[编辑本段]对数函数
一般地,函数y=log(a)X,(其中a是常数,a>0且a不等于1)叫做对数函数
它实际上就是指数函数的反函数,可表示为x=a^y。因此指数函数里对于a的规定,同样适用于对数函数。
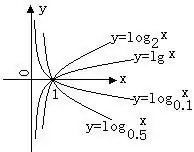
右图给出对于不同大小a所表示的函数图形:
可以看到对数函数的图形只不过的指数函数的图形的关于直线y=x的对称图形,因为它们互为反函数。
(1) 对数函数的定义域为大于0的实数集合。
(2) 对数函数的值域为全部实数集合。
(3) 函数图像总是通过(1,0)点。
(4) a大于1时,为单调增函数,并且上凸;a小于1大于0时,函数为单调减函数,并且下凹。
(5) 显然对数函数无界。
对数函数的常用简略表达方式:
(1)log(a)(b)=log(a)(b)
(2)lg(b)=log(10)(b)
(3)ln(b)=log(e)(b)
对数函数的运算性质:
如果a〉0,且a不等于1,M>0,N>0,那么:
(1)log(a)(MN)=log(a)(M)+log(a)(N);
(2)log(a)(M/N)=log(a)(M)-log(a)(N);
(3)log(a)(M^n)=nlog(a)(M) (n属于R)
(4)log(a^k)(M^n)=(n/k)log(a)(M) (n属于R)
对数与指数之间的关系
当a大于0,a不等于1时,a的X次方=N等价于log(a)N
log(a^k)(M^n)=(n/k)log(a)(M) (n属于R)
换底公式 (很重要)
log(a)(N)=log(b)(N)/log(b)(a)= lnN/lna=lgN/lga
ln 自然对数 以e为底 e为无限不循环小数
lg 常用对数 以10为底
对数函数的常用简略表达方式:
(1)常用对数:lg(b)=log(10)(b)
(2)自然对数:ln(b)=log(e)(b)
e=2.718281828... 通常情况下只取e=2.71828 对数函数的定义
对数函数的一般形式为 y=㏒(a)x,它实际上就是指数函数的反函数(图象关于直线y=x对称的两函数互为反函数),可表示为x=a^y。因此指数函数里对于a的规定(a>0且a≠1),同样适用于对数函数。
右图给出对于不同大小a所表示的函数图形:
可以看到对数函数的图形只不过的指数函数的图形的关于直线y=x的对称图形,因为它们互为反函数。
[编辑本段]性质
定义域:(0,+∞)值域:实数集R
定点:函数图像恒过定点(1,0)。
单调性:a>1时,在定义域上为单调增函数,并且上凸;
0<a<1时,在定义域上为单调减函数,并且下凹。
奇偶性:非奇非偶函数,或者称没有奇偶性。
周期性:不是周期函数
零点:x=1
注意:负数和0没有对数。
两句经典话:底真同对数正
底真异对数负
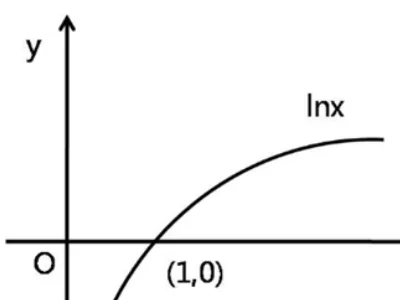
f(x)= lnx的图像是什么样子?
f(x)=lnx的函数图像是一条过I,IV象限的对数函数曲线,是一条定义域在(0,+∞),值域在R上,单调递增的曲线。曲线经过(1,0),且向上凸起。lnx的性质:
1、定义域为x∈(0,+∞),值域为(-∞,+∞),图形分布在一四象限;为单调递增,非奇非偶。
2、从导数来看单调性看起来更快y'=lnx-1)/lnx,由此明显地以(e,+∞)增加,以(1,e)(0,1)减少。y<0(同样靠近1的左侧的话,负数就会无限大,但是为什么小于0是指示器的法则)。
值域在函数经典定义中,因变量改变而改变的取值范围叫做这个函数的值域,在函数现代定义中是指定义域中所有元素在某个对应法则下对应的所有的象所组成的集合。自然对数是以常数e为底数的对数,记作lnN(N>0)。在物理学,生物学等自然科学中有重要的意义,一般表示方法为lnx。数学中也常见以logx表示自然对数。